Deciphering Enigmas in the Gravitational Collapse of Gravitational Waves

Black holes come into existence through a process referred to as gravitational collapse. This involves the fundamental contraction of a cosmological object, driven by the gravitational force causing matter to collapse inward, converging towards the center of gravity within the object.

The formation of a black hole from a collapsing object hinges on the distinct properties of that object. In certain scenarios, an object may teeter near the threshold, struggling to determine whether it will evolve into a black hole. Such a collapse scenario leads to what is known as critical phenomena.

For decades, physicists have endeavored to comprehend critical phenomena in gravitational collapse, as certain characteristics parallel those observed in other established physical systems. A recent publication in Physical Review Letters, authored by an international research collaboration centered at Bowdoin College in the United States, along with contributions from institutes in Germany, Prague, the U.K., and Portugal, achieved consensus through three independently conducted numerical simulations. This collaborative effort not only confirmed the existence of these phenomena but also addressed longstanding questions within this realm of study.

Thomas W. Baumgarte, a co-author of the paper, conveyed that critical phenomena in gravitational collapse, observed near the initiation of black-hole formation, were initially documented by Matt Choptuik approximately 30 years ago. These effects garnered significant interest from researchers across various physics disciplines due to their resemblance to critical phenomena in other areas, such as phase transitions in statistical physics. Moreover, the study of these phenomena addresses fundamental inquiries pertaining to the properties of general relativity, adding to the widespread attention from researchers in diverse physics fields.

Critical gravitational collapse exhibits two captivating properties: universality and self-similarity. Universality implies that regardless of the initial conditions of a calculation, as the formation of a black hole becomes imminent, the solution remains constant. In contrast, self-similarity denotes that this universal solution will replicate identical patterns as the physical scale undergoes reduction.

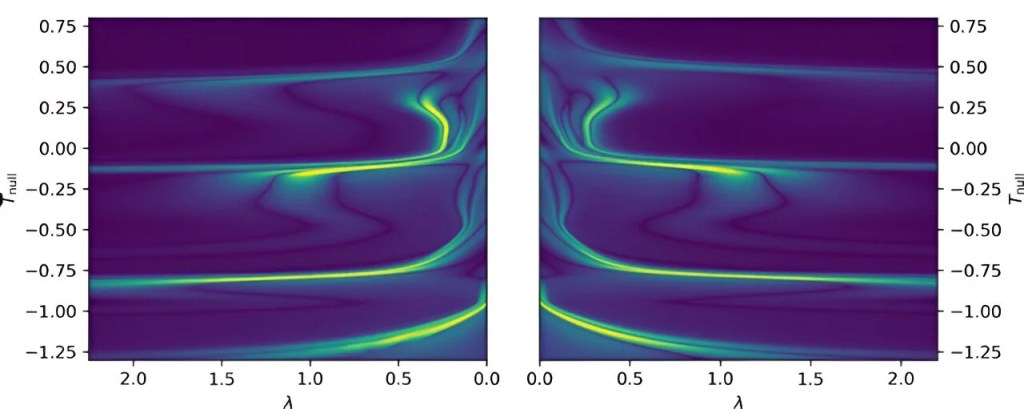
According to Baumgarte, Choptuik initially conducted calculations involving a scalar field as a matter source. Following this, Abrahams and Evans reported similar effects in the gravitational collapse of gravitational waves, which essentially involves pure gravity without any matter. A notable distinction is that Choptuik could assume spherical symmetry, but gravitational waves cannot exist in such symmetry. Therefore, Abrahams and Evans had to abandon the assumption of spherical symmetry. Unfortunately, reproducing these latter results has proven challenging, with some numerical codes either failing or yielding results seemingly at odds with those reported by Abrahams and Evans.

After encountering seemingly conflicting results in the 1990s, the understanding of the critical collapse of “pure gravity” persisted as an unsolved puzzle for nearly three decades. However, in a recent development, three distinct research groups undertook independent numerical simulations of this collapse, employing codes that they developed independently.

Baumgarte explained that the three codes employed for the simulations all tackle Einstein’s equations of general relativity. However, they employ entirely distinct numerical strategies, such as spectral methods versus finite-difference methods. Additionally, they differ in their use of Cartesian coordinates versus spherical polar coordinates, adopt different gauge conditions, and make varied choices for the “slicing condition,” which dictates the rate at which time advances in the codes.

Baumgarte and his colleagues pursued a primary goal in their recent study: to collaboratively scrutinize the three numerical simulations conducted by separate research teams. The paper reflects a joint effort, aiming to unite these independent research endeavors and provide fresh insights into the intricacies of gravitational collapse.

Baumgarte highlighted a significant initial discovery in their study, emphasizing that, despite the various numerical disparities among the codes, they consistently yielded congruent results for the critical collapse of gravitational waves. This consistency instilled confidence in the validity of the findings, ruling out the possibility of numerical artifacts. Notably, the study underscored the critical importance of selecting an appropriate slicing condition. A widely used alternative choice, successful in numerous numerical relativity simulations, proved ineffective in this specific case, elucidating the reasons behind previous unsuccessful attempts to address this problem.

Remarkably, the researchers discovered a lack of evidence supporting the property of universality in their three distinct numerical simulations. In simpler terms, initiating the simulations with different initial data yielded divergent outcomes as the system approached the formation of a black hole.

Baumgarte explained that their findings contribute to resolving a previously puzzling aspect. Earlier studies had noted disparities from the results reported by Abrahams and Evans, creating apparent contradictions. However, these studies utilized different initial data. The disagreement between the results, therefore, is not contradictory when considering that universality is not evident, challenging the assumption that all simulations should converge under the same conditions.

The researchers, despite finding no support for universality, did identify approximate indications of self-similarity. Intriguingly, the self-similarity observed in this context did not seem to be precisely exact, in contrast to what was observed in the case of critical collapse in spherical symmetry.

In the 1990s, Abrahams and Evans similarly reported non-exact self-similarity. The current findings align with these earlier results, hinting that deviations from exact self-similarity might be associated with the absence of spherical symmetry.

Baumgarte and his colleagues’ recent work has the potential to open avenues for fresh numerical and theoretical investigations into the critical collapse of gravitational waves. These endeavors could propel physicists toward a deeper understanding and reframing of this captivating physical phenomenon, which plays a crucial role preceding the formation of black holes.

Baumgarte acknowledged that, although their work has addressed several uncertainties regarding the critical collapse of gravitational waves, it has also prompted new questions. One aspect of this is the discovery of approximately self-similar solutions for certain families of initial data but not for others. The nature of the “threshold solution” for these other families remains unclear, introducing avenues for future research to delve deeper into these unresolved aspects.

Additionally, it would be beneficial to conduct simulations with enhanced precision near the onset of black-hole formation. This could involve employing numerical codes with improved resolution or incorporating other enhancements to investigate whether a universal critical solution emerges with a level of fine-tuning beyond what has been achieved thus far.

Baumgarte expressed the team’s intention to explore the factors influencing deviations from exact self-similarity and ascertain whether these deviations are directly associated with the absence of spherical symmetry.

Resources

1. ^NEWSPAPER Fadelli, I. & Phys.org. (2023, November 15). Study resolves puzzles in gravitational collapse of gravitational waves. Phys.org. [Phys.org]
2. ^JOURNAL Baumgarte, T. W., Brügmann, B., Cors, D., Gundlach, C., Hilditch, D., Khirnov, A., Ledvinka, T., Renkhoff, S., & Fernández, I. S. (2023). Critical phenomena in the collapse of gravitational waves. Physical Review Letters, 131(18). [Physical Review Letters]